Introduzione al Teorema di Bayes

Beh, amico mio, preparati a fare un salto nel mondo della probabilità! Il Teorema di Bayes è come un supereroe che ti aiuta a capire la probabilità di un evento, dato che sai qualcosa di altro che potrebbe essere collegato a quell’evento. Immaginalo come un detective che indaga su un crimine: analizza le prove per arrivare alla soluzione più probabile.
Componenti chiave del Teorema di Bayes, Bayesian
Ok, ora che hai un’idea generale, diamo un’occhiata alle componenti chiave di questo teorema:
- Probabilità a priori: È la probabilità di un evento prima di avere nuove informazioni. È come il tuo “istinto” iniziale, la tua ipotesi di base. Ad esempio, se lanci una moneta, la probabilità a priori di ottenere testa è 1/2, perché non hai altre informazioni.
- Probabilità condizionata: È la probabilità di un evento, dato che sai che un altro evento è già accaduto. È come quando il detective trova una nuova prova che cambia il suo pensiero sul caso. Ad esempio, la probabilità condizionata di ottenere testa, sapendo che il lancio precedente è stato croce, è ancora 1/2, perché i lanci di moneta sono indipendenti.
- Probabilità a posteriori: È la probabilità di un evento dopo aver considerato nuove informazioni. È come la conclusione finale del detective, dopo aver analizzato tutte le prove. Ad esempio, se vedi che la moneta è truccata e tende a dare più testa che croce, la probabilità a posteriori di ottenere testa sarà maggiore di 1/2.
Esempio pratico del Teorema di Bayes
Immagina di essere a una festa e vedi un amico che sta bevendo un drink. Sai che il tuo amico è un grande fan della birra, ma non sei sicuro se stia bevendo birra o vino.
* La probabilità a priori che il tuo amico stia bevendo birra è alta, perché sai che gli piace la birra.
* La probabilità condizionata che il tuo amico stia bevendo birra, dato che vedi un bicchiere di colore chiaro, è bassa, perché i bicchieri di vino sono spesso di colore chiaro.
* La probabilità a posteriori che il tuo amico stia bevendo birra, dato che sai che gli piace la birra e vedi un bicchiere di colore chiaro, è ancora alta, perché la tua conoscenza precedente sul suo gusto per la birra è forte.
Importanza del Teorema di Bayes nell’inferenza statistica e nell’apprendimento automatico
Il Teorema di Bayes è una bomba nel mondo della statistica e dell’apprendimento automatico! Viene utilizzato per aggiornare le nostre credenze sulla base di nuove informazioni. È come un meccanismo di apprendimento automatico che ci aiuta a migliorare le nostre previsioni e decisioni.
Ad esempio, il Teorema di Bayes è usato nei filtri antispam per identificare le email indesiderate, nei sistemi di diagnosi medica per identificare le malattie e nei motori di ricerca per fornire risultati pertinenti.
Applicazioni del Teorema di Bayes: Bayesian

Il Teorema di Bayes, con la sua eleganza matematica, non è solo una formula astratta. È uno strumento potente che trova applicazioni in un’ampia gamma di settori, dalla medicina alla finanza, dall’ingegneria all’informatica. La sua capacità di aggiornare le probabilità basandosi su nuove informazioni lo rende uno strumento prezioso per la risoluzione di problemi in situazioni di incertezza.
Applicazioni del Teorema di Bayes in Medicina
In medicina, il Teorema di Bayes è utilizzato per valutare la probabilità che un paziente abbia una particolare malattia, dato un risultato di un test medico. Ad esempio, se un test per il cancro al seno è positivo, il Teorema di Bayes può aiutare a determinare la probabilità che la paziente abbia effettivamente il cancro, considerando la sensibilità e la specificità del test, nonché la prevalenza del cancro nella popolazione.
Applicazioni del Teorema di Bayes in Finanza
Nel campo della finanza, il Teorema di Bayes è utilizzato per valutare il rischio e il rendimento degli investimenti. Ad esempio, un gestore di portafoglio può utilizzare il Teorema di Bayes per aggiornare le sue previsioni sul rendimento di un’azione, considerando le nuove informazioni sul mercato, come i risultati finanziari dell’azienda o le variazioni dei tassi di interesse.
Applicazioni del Teorema di Bayes in Ingegneria
In ingegneria, il Teorema di Bayes è utilizzato per la progettazione di sistemi di controllo e di diagnostica. Ad esempio, in un sistema di controllo automatico, il Teorema di Bayes può essere utilizzato per aggiornare le stime dello stato del sistema, considerando le misure del sensore e il rumore del sistema.
Applicazioni del Teorema di Bayes in Informatica
Nell’informatica, il Teorema di Bayes è utilizzato per lo sviluppo di algoritmi di apprendimento automatico, come i filtri antispam e i sistemi di riconoscimento facciale. Ad esempio, un filtro antispam può utilizzare il Teorema di Bayes per classificare le email come spam o non spam, considerando le parole chiave e le caratteristiche dell’email.
| Applicazione | Problema | Vantaggi |
|---|---|---|
| Diagnostica Medica | Valutare la probabilità di una malattia dato un risultato di un test | Migliora l’accuratezza della diagnosi e riduce i falsi positivi e negativi |
| Gestione del Rischio Finanziario | Valutare il rischio e il rendimento degli investimenti | Aiuta a prendere decisioni di investimento più informate e a ridurre il rischio |
| Controllo Automatico | Stimare lo stato di un sistema in presenza di rumore | Migliora la precisione del controllo e la robustezza del sistema |
| Apprendimento Automatico | Classificare i dati in base a caratteristiche specifiche | Permette di sviluppare algoritmi di apprendimento automatico più efficienti e accurati |
Approfondimenti sul Teorema di Bayes
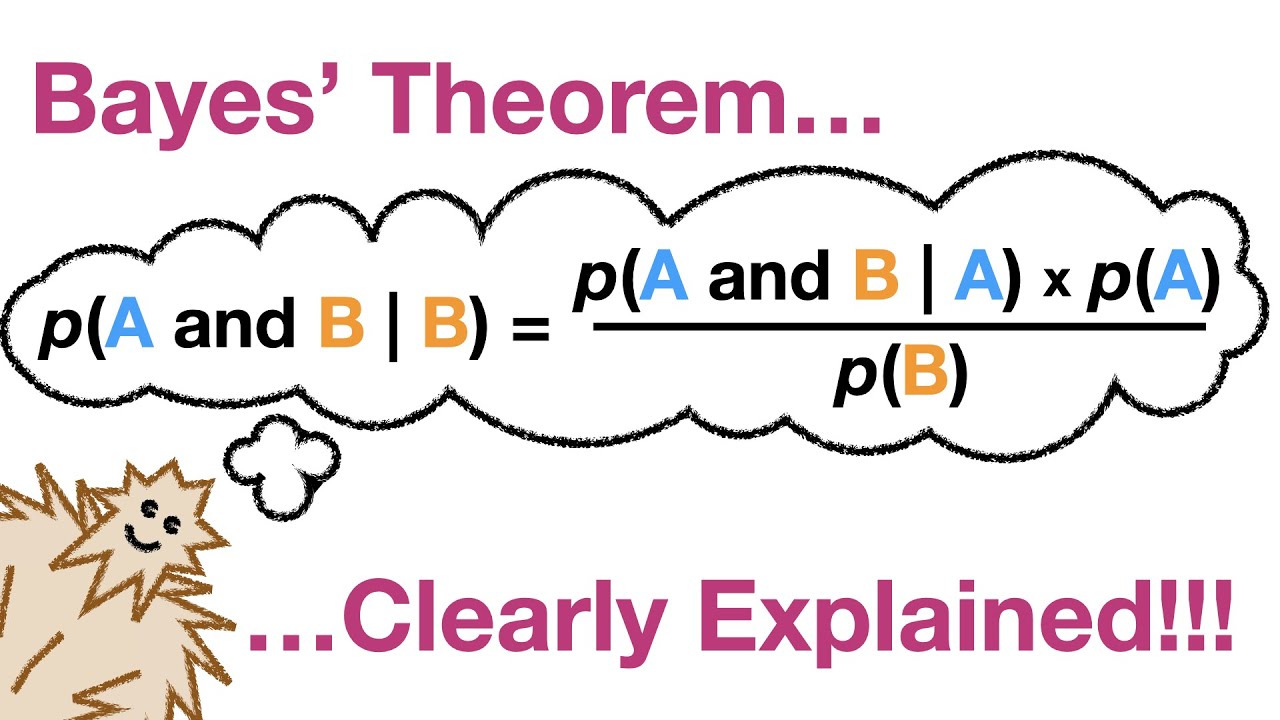
Il Teorema di Bayes è un potente strumento per l’inferenza statistica, ma il suo utilizzo e la sua interpretazione possono essere complessi. In questa sezione, esploreremo diverse interpretazioni del teorema, confronteremo i metodi bayesiani con i metodi frequentisti, e analizzeremo i vantaggi e gli svantaggi dell’utilizzo del teorema di Bayes.
Interpretazioni del Teorema di Bayes
Il teorema di Bayes può essere interpretato in due modi principali: l’interpretazione frequentista e l’interpretazione bayesiana.
- Interpretazione frequentista: Questa interpretazione si basa sulla frequenza relativa degli eventi. La probabilità di un evento è vista come la frequenza relativa con cui l’evento si verifica in un numero infinito di prove. In questo contesto, il teorema di Bayes viene utilizzato per aggiornare la probabilità di un evento in base a nuove informazioni.
- Interpretazione bayesiana: Questa interpretazione si basa sul concetto di grado di credenza. La probabilità di un evento è vista come il grado di fiducia che abbiamo nell’evento, dato il nostro stato di conoscenza attuale. In questo contesto, il teorema di Bayes viene utilizzato per aggiornare il nostro grado di credenza in un evento in base a nuove informazioni.
Confronto tra metodi bayesiani e frequentisti
I metodi bayesiani e frequentisti sono due approcci diversi all’inferenza statistica.
- Metodi frequentisti: Questi metodi si basano sulla frequenza relativa degli eventi e utilizzano test di ipotesi e intervalli di confidenza per inferire le proprietà della popolazione.
- Metodi bayesiani: Questi metodi si basano sul concetto di grado di credenza e utilizzano distribuzioni di probabilità per descrivere l’incertezza sulle proprietà della popolazione.
| Metodo | Principio | Strumenti | Obiettivo |
|---|---|---|---|
| Frequentista | Frequenza relativa degli eventi | Test di ipotesi, intervalli di confidenza | Inferire le proprietà della popolazione |
| Bayesiano | Grado di credenza | Distribuzioni di probabilità | Aggiornare il grado di credenza in base a nuove informazioni |
Vantaggi e svantaggi del Teorema di Bayes
Il teorema di Bayes ha diversi vantaggi e svantaggi.
- Vantaggi:
- Consente di aggiornare la nostra conoscenza in base a nuove informazioni.
- È flessibile e può essere applicato a una vasta gamma di problemi.
- Fornisce un modo formale per combinare informazioni provenienti da diverse fonti.
- Svantaggi:
- Può essere complesso da implementare, soprattutto per problemi complessi.
- Richiede la specifica di una distribuzione a priori, che può essere soggettiva.
- Può essere sensibile alla scelta della distribuzione a priori.
Casi in cui il Teorema di Bayes è particolarmente utile
Il teorema di Bayes è particolarmente utile in situazioni in cui:
- Si dispone di informazioni a priori sul problema.
- Si desidera aggiornare la nostra conoscenza in base a nuove informazioni.
- Si desidera combinare informazioni provenienti da diverse fonti.
Casi in cui il Teorema di Bayes potrebbe non essere la scelta migliore
Il teorema di Bayes potrebbe non essere la scelta migliore in situazioni in cui:
- Non si dispone di informazioni a priori sul problema.
- I dati sono scarsi o di bassa qualità.
- Il problema è troppo complesso per essere gestito con il teorema di Bayes.
Bayesian analysis thrives on the constant updating of beliefs based on new evidence, much like how Mike Lynch’s philosophy of autonomy encourages individuals to continuously adapt and refine their approaches to achieving success. Mike Lynch autonomy emphasizes the importance of self-direction and ownership, aligning perfectly with the iterative nature of Bayesian thinking.
This dynamic interplay between prior knowledge and incoming data allows for a more nuanced and accurate understanding of the world, mirroring the adaptability and flexibility championed by Lynch’s philosophy.
Bayesian methods, often used in machine learning, are a powerful tool for updating beliefs based on new evidence. One notable figure in the field is mike linch , whose work on probabilistic programming has significantly advanced Bayesian inference. The ability to model complex systems with uncertainty and learn from data is a key strength of Bayesian approaches, making them increasingly relevant in various domains.
